THE EGYPTIAN CALENDAR

In ancient Egypt the year was divided into three seasons, each about four lunar months in length. The first season was called akhet or "inundation," approximately July to October, and was the time when the Nile rose and overflowed the fields. The second was peret or "coming forth," approximately November to February, when the fields emerged again from the flood waters and seeding, tilling, and growth of crops took place. The third was schemu or "deficiency," approximately March to June, when harvest was followed by the time of low water before the next inundation.63 The recognition of these seasons, based upon climatic and agricultural factors, was undoubtedly very old. 

At least bJy the start of the Old Kingod om astronomical knowledgde was well advanced, and astronomical factors related to the calendar were soon recognized. At an early time the year probably started with the lunar month which began after the Nile began to rise. The rise of the river normally began at Aswan in late May or early June, and was about ten days later at Memphis. Coming thus in the summer, the period of the great inundation included the time of the summer solstice (§32). At about the same time a celestial phenomenon took place which also attracted attention in Egypt at an early date, namely the heliacal rising of Sirius. Sirius is the brightest of all the fixed stars, and was known as Sothis in the Greek spelling of its Egyptian name (Sopdu), and also as Canicula, the Dog Star. After being hidden below the horizon for seventy davs, 1 O O -J Sirius reappeared in the east just before sunrise (heliacal rising), and this took place at about the beginning of the annual inundation of the Nile.64 It may be added that the heliacal risings of thirty-six stars or constellations (Orion, etc.), which occurred approximately every ten days, were also noted and used, under the name of decans, to mark as many periods of the year.65 Returning to Sirius, the length of the year from heliacal rising to heliacal rising of Sirius was very close to the length of the solar year (only twelve minutes shorter) which, as we have seen (§33), is now calculated as 365.24219879 days. In Table 5 the length of the Sirius-year is shown at several intervals.

Thus, in 3231 B.C., the Sirius-year was 365 !/4 days in length, exactly the same as the value taken for the Julian year (§144), and it became longer only very slowly. In terms of the Julian calendar, the reappearance of Sirius at dawn in the latitude of Memphis fell on July 19 from the fifth millennium to the second half of the first millennium B.C.—i.e., throughout the whole course of ancient Egyptian history—and then gradually moved to July 20. In the same period of four thousand years, from 4231 to 231 B.C., in which the heliacal rising of Sirius moved later by one day in comparison with the Julian year, the summer solstice, on the other hand, moved thirty-one days earlier in the Julian year, namely from July 28 in the year 4231 to June 27 in the year 231 B.C. In accordance with these changes, the summer solstice took place in Memphis in the forty-third century (4300-4201) B.C., nine days after the heliacal rising of Sirius; in the thirty-first century (3100—3001) B.C., on the same day, i.e., on July 19; and in each century thereafter fell back another eighteen and two-thirds hours.66 Thus, if the great summer inundation was originally taken as signaling the beginning of a new year in an agriculturally oriented reckoning, these two celestial events which fell within the same period, the summer solstice and the heliacal rising of Sirius which was at one time exactly coincident therewith, were available to provide a more precise point of beginning in an astronomically oriented reckoning. Since the reappearance of Sirius at sunrise was the more readily observable event, it is probable that this was what was first utilized. In fact, an inscription of the First Dynasty probably reads: "Sothis, the opener of the year; the inundation."67 Since the event of the heliacal rising had the remarkable stability which we have noted, it provided a fixed point of reference for a very long time, as we shall see (§§41, 45—48).

The Three Calendars

Since the year was composed of lunar months, the calendar whose probable origins have just been described may be called a lunar calendar; since the beginning of the year was fixed by reference to a star, it may be described more specifically as a lunistellar calendar. A year composed of twelve lunar

months, ordinarily alternating between twenty-nine and thirty days in length, makes 354 days, which is approximately eleven days short of the solar year. To keep the calendar year beginning in the spring, in general, and at the time of the heliacal rising of Sothis in particular, it must have been necessary to insert an additional month every three years or so. It seems that when this occurred, the intercalary month was put at the head of the new lunar year. In our own calendar when an extra day is added to make a year of 366 rather than 365 days it is called a "leap" year (§144), and in any calendar in which there is intercalation of a day or a month the same term may be used. It is believed that this calendar, as just described, was the original lunar or "natural" calendar of Egypt and was in use before and in the early dynastic period and long thereafter.68 Being controlled by the rising of Sirius to determine the new year, it was "fixed" and, as such was the calendar for religious affairs and everyday life.

Alongside the "natural" calendar of Egypt just described (§39), there was established for administrative, government, and business purposes a "public" or "civil" calendar.69 Whether it was by averaging a series of the lunar years or by counting the days between the heliacal risings of Sirius at the time of the inundation, it became known that the true length of the year to the nearest number of days was 365. The disadvantages of a year composed now of twelve and again of thirteen lunar months must have been evident, and the knowledge of the year's length as 365 days made possible the new system. After the analogy of the lunar system the year was still divided into three seasons and twelve months, but for the sake of simplicity and regularity each month was made thirty days in length. This left a shortage of only five days and, after the example of the intercalated month at the beginning of the lunar vear, five extra davs o o ^ (epagomenal days) were inserted before the new year. These were considered holidays in celebration of the "birthdays" of the gods Osiris, Seth, and Horus, and of the goddesses Isis and Nephthys. Since the months were no longer kept in relationship to the real moon but were fixed units in the solar year instead, this may be recognized as essentially a solar calendar, and since the units have an artificial regularity it may be called a "schematic" calendar. This system was introduced, there is reason to believe, between c. 2937 and c. 2821 B.C. and from then on served as the standard civil calendar of Egypt.70

The civil calendar of 365 days was still, however, not in exact agreement with the solar year since the latter is actually closer to 3651/4 days in length. At the outset, it may be assumed, the first day of the civil year coincided with the heliacal rising of Sothis. After four years it would begin on the day before the rising of Sothis, after eight years, two days before, and so on, and was thus a "shifting" or "sliding" calendar. Only after 1,460 years would the beginning of the civil year have moved all the way around the cycle to coincide once again with the rising of Sothis. Since the original lunar calendar was periodically corrected to keep its beginning point in connection with the heliacal rising of Sothis, the civil calendar gradually diverged more and more from the lunar calendar. It is assumed that this divergence would have become apparent by, say, 2500 B.C., and that around that time a second lunar calendar was introduced which was thereafter maintained in substantial harmony with the civil year with such intercalation as was necessary, and, as before, was used to determine religious celebrations and duties.7' Thus, from that time on, Egypt actually had no less than three calendars and three calendar years, and all of these continued in use throughout the remainder of ancient Egyptian history.72 From here on we are chiefly concerned with the standard civil calendar.

The Months

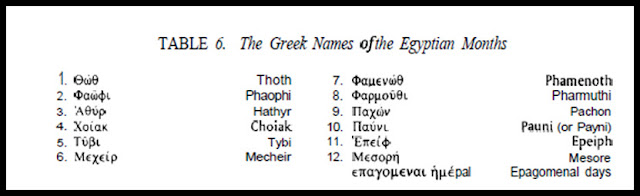
From early times the designation of the months of the Egyptian year was by number as, e.g., on the Palermo Stone, "Fourth month, thirteenth day;"73 or by number within one of the three seasons as, e.g., on a stela of Thutmose III, "Second month of the second season, tenth day."74 The months were also given names, however, and in the Hellenistic o 7 ' and Roman periods these appear in Greek as shown in Table 6.

The preceding tabulation represents the year as beginning with the month Thoth, with Thoth 1 as New Year's day, which was the usual reckoning. There was also a reckoning from Mecheir 1. The latter is encountered in the papyri where it is indicated as cb? al rrpoaoSoi. f| Trpoao8os means "a going to" and is used, mostly in the plural al irpoaoSoi, for "the public revenues." Hence, (05 al TTpoaoSoi means "according to the financial calendar." It was also possible to date from a given point in the king's reign and examples are found, varying from reign to reign, so the reference point probably represented the anniversary of the king's accession.75 From here on we shall be chiefly concerned with the year beginning Thoth 1. The standard civil calendar beginning Thoth 1 is found, however, in two forms, the earlier form with a shifting year, the later form with a fixed year.

The Standard Civil Calendar with a Shifting Year

In accordance with the nature of the standard civil calendar (§40), the months listed above had each thirty days, and the five days inserted before the beginning of the new year made a total year length of 365 days. Since the total was one-fourth day short of the solar year, in four years the calendar fell back one whole day (§41). This means that in each four years Thoth 1 fell one day earlier. The equivalents in Table 7, for example, have been established in the Ptolemaic period.

The shifting or wandering year (Wandeljahr) just described and the long Sothic cycle through which it moved continued to be observed for a long time. A clear statement of how the Egyptian civil year (annus civilis) is not related to the moon, has 365 days, and moves to a fresh beginning in 1,461 years, is given by Censorinus, who also says that this Sothic period is called a "great year" (annus magnus) or "year pertaining to the Dog Star" (annus canicularis or KUviKog).77 Writing in A.D. 238 he says78 that in that year the Egyptian Thoth 1 fell on VII Kal lul. = June 25 (for such dates see §141 below), and that one hundred years before when Antoninus Pius was consul for the second time along withBrutius Praesens, i.e., in A.D. 139 (for dating by consuls see below §§172ff.), it fell on XII Kal. Aug = July 21, a reference probably to be corrected to XIII Kal. Aug = July 20 which would agree with the date of the heliacal rising ol Sirius in that period (§38). Thus the year beginning Thoth 1 = July 20, A.D. 139 was evidently the first year of a new Sothic cycle. Counting forward from 139/140 as the first year, the year 238/239 was in fact the one hundredth year, and in the one hundred years the beginning of the calendar year had moved twenty-five days from July 20 to June 25. Counting backward 1,460 years from  139/140 A.D., the first year of the preceding Sothic cycle would have been the year from July 19, 1321, to July 18, 1320 B.C., and similar cyclic points prior to that would have been 2781/2780 and 4241/4240 B.C.79 It is the date of 4241 B.C. which James Henry Breasted once called "the earliest fixed date in the history of the world."80

The Sothic cycle, whose first year was July 19, 1321, to July 18, 1320 B.C., is probably also attested by Theon, who wrote in the fourth century A.D. Expressly using the Egyptian shifting year, Theon reckons 1,605 years "from Menophres" to the end of the era of Augustus. The era of Diocletian began on Aug 29, A.D. 284, and the last year of the Augustan era was accordingly 283/284. One thousand six hundred and five of the shorter shifting O J O Egyptian years are equal to 1,604 Julian years less thirty-six days; and 1,604 years before A.D. 283/284 brings us back to 1321/1320 B.C. Thus reckoning "from Menophres" is probably the same as the reckoning from the Sothic period which began in 1321/1320 B.C. As for the name Menophres (Mevo<t>pT|c;), it has been thought possible to recognize in it the praenomen of Ramses I, read asMn-ph-r,81 but the preferred date for the reign of Ramses I is now 1295—1294 B.C.  so the connection with this king is no longer likely. There is also reference to the Sothic cycle in Clement of Alexandria where he says that Moses went forth from Egypt three hundred and forty-five years before the Sothic period ).82 After this, dates are given out of Greek legendary history down to the first year of the first Olympiad, and if these figures were intact and complete it would again be possible to make a calculation relative to the Sothic date, but since they probably are not, this need not be considered further.83

The Standard Civil Calendar with a Fixed Year

In contrast to this "wandering" year which existed for so long in the standard civil calendar of Egypt, we turn to what is known as the fixed Alexandrian year, which finally prevailed. In 22 B.C. Augustus introduced the Julian calendar (§§143f.) into Egypt and reformed the Egyptian calendar to bring it into harmony therewith. Every fourth year, in the year preceding the leap year of the Julian calendar—i.e., in A.D. 3/4, 7/8, etc.—a sixth epagomenal day was added in the Egyptian calendar. With this stabilization, the first day of Thoth was kept permanently on Aug 29 (where it fell at the time of the reform), except in the intercalary year when the addition of the sixth epagomenal day put Thoth 1 on Aug 30 and put each succeeding day through Phamenoth 4 = Feb 29 one day later than in the common years. After the intercalary year the calendar returns to its normal relation, and always Phamenoth 5 = Mar I.84 T Shows this fixed Egyptian calendar, with the number of days in the Egyptian months and the equivalent Julian dates for the months both in an Egyptian common year and in an Egyptian intercalary year. At the point of the transition from the portion of the calendar affected by the intercalary year to the part following, the presentation is amplified to show the details of the change. This is the calendar still observed by the Copts in Egypt.85

Notes

63Henri Frankfort, Kingship and the Gods (Chicago: University of Chicago Press, 1948), 367 n. 3; PCAE 32.

64Finegan, Myth and Mystery, 41—42.

65Wilhelm Gundel, Dekane und Dekansternbilder (Studien der Bibliotek Warburg 19; Gliickstadt and Hamburg: J. J. Augustin, 1936).

66Meyer, Aeyryptische Chronologic, 14—15, 23.

67PCAE 32, 34,74 n. 22.

68PCAE 30-50, 53.

69 Hermann Kees, Der Gotterglaube im alien Agypten (Berlin: Akademie-Verlag, 1977),

259-260; Eugen Strouhal, Life of the Ancient Egyptians, 239-241.

70PCAE S3. This Egyptian calendar consisting of twelve months of thirty days each and five additional days at the end of each year has been called by O. Neugebauer (The Exact Sciences in Antiquity [Princeton, N.J.: Princeton University Press, 1952], 81) "the only intelligent calendar which ever existed in history."

71£B (1987), 15: 464.

72PCAE 54, 56.

76A. Bouche-Leclercq, Histoire des Lagides (4 vols.; Paris: E. Leroux, 1903-1907), 3: 384-407.

7718.10; Censorial De die natali liber, ed. F. Hultsch (Leipzig: Teubner, 1867), 38.

7821.10, ed. Hultsch, 46.

79Meyer, Aegyptische Chronologic, 23-29; Laszlo Kakosy, "Sothis," LA 5: 1110-1117; Ulrich Luft, "Sothisperiode," LA 5: 1117-1124.

80Breasted, A History of Egypt from the Earliest Times to the Persian Conquest (New York: Scribner, 1905), 26.

81 Richard A. Parker,JNES 16 (1957): 39-43; M. B. RowtonJCS 13 (1959): 8-9; JNES 19 (1960): 15-22; Jaroslav VernyJEA 47(1961): 150-152. slStromata 1.21, 136.

85Meyer, Aegyptische Chronologic, 30.

84George Milligan, Selections from the Greek Papyri, xviii; Bernard R Grenfell and Arthur S. Hunt, OxyP 12: 291; cf. f. C. Skeat, Mizraim 8 (1937): 21, who says wrongly, I think, that Phamenoth 6 always equals Mar 1.

85Strouhal, Life of the Ancient Egyptians, 240.

Written by Jack Finegan in "Handbook of Biblical Chronology", Hendrickson Publishers, USA, 1998, excerpts pp. 18-25. Digitized, adapted and illustrated to be posted by Leopoldo Costa.